Fast Algorithms and Integral Equation Methods (CS 598APK) Fall 2024

What	Where
Time/place	Tue/Thu 11:00am-12:15pm 1302 Siebel / Catalog
Class URL	https://bit.ly/fastalg-s24
Class recordings	Watch »
Discussions	Discuss »
Calendar	View »

Assignments

Project Presentations

Tuesday May 7

Jay Woo: Accelerating the NuFFT
Yue Yuan: Embedded Boundary Integral Method (EBI) for the Incompressible Navier-Stokes equations
Yu-Hsiang Lan: Coupling of Integral Methods for Interior Heat Source
Zirui Wang: High performance implementation of fast hilbert transformation
Qi Jian Lim: Electric Field Integral Equation in 3-D

Thursday May 9

Addison Alvey-Blanco: Fused FMM
Hirish Chandrasekaran: Evaluation of Layer Potentials Close to Boundary
Haoen Lei: Reimplement High-order discretization of a stable time-domain integral equation for 3D acoustic scattering
Gonzalo Nunez Munoz: MoM for Quasi-periodic structures.
Srikumar Balasubramanian: Layer potential solution to an internal dirichlet problem: comparisons with immersed boundary solution

Why you should take this class

The numerical solution of a 3D scattering problem

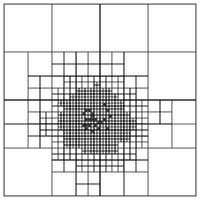
A quadtree as used in a Fast Multipole Method

Many of the algorithms of introductory scientific computing have super-linear runtime scaling. Gaussian elimination or LU decomposition are good examples, their runtime scales as $O(n^3)$ with the number of unknowns $n$. Even simple matrix-vector multiplication exhibits quadratic scaling. Problems in scientific computing, especially those arising from science and engineering questions, often demand large-scale computation in order to achieve acceptable fidelity, and such computations will not tolerate super-linear, let alone quadratic or cubic scaling.

This class will teach you a set of techniques and ideas that successfully reduce this asymptotic cost for an important set of operations. This leads to these techniques being called "fast algorithms". We will begin by examining some of these ideas from a linear-algebraic perspective, where for matrices with special structure, large cost gains can be achieved. We will then specialize to PDE boundary value problems, which give rise to many of the largest-scale computations. We will see that integral equations are the natural generalization of the linear-algebraic tools encountered earlier, and we will understand the mathematical and algorithmic foundations that make them powerful tools for computation. All throughout, we will pay much attention to the idea of representation–i.e. the choice of what the numerical unknowns of the system to be solved should be.

Instructor

Andreas Kloeckner

Andreas Kloeckner

(Instructor)

Email: andreask@illinois.edu

Office: 4318 Siebel

Course Outline

Note: the section headings in this tree are clickable to reveal more detail.

Introduction
- Notes
- Notes (unfilled, with empty boxes)
Dense Matrices and Computation
Tools for Low-Rank Linear Algebra
- Low-Rank Approximation: Basics
- Low-Rank Approximation: Error Control
- Reducing Complexity
- Demo: Interpolative Decomposition
- Demo: Randomized SVD
- Demo: Rank-Revealing QR
Rank and Smoothness
- Local Expansions
- Multipole Expansions
- Rank Estimates
- Proxy Expansions
- Demo: Checking Rank Estimates
- Demo: Multipole and Local Expansions
- Demo: Skeletonization using Proxies
Near and Far: Separating out High-Rank Interactions
- Ewald Summation
- Barnes-Hut
- Fast Mutipole
- Direct Solvers
- The Butterfly Factorization
- Demo: Butterfly Factorization
Outlook: Building a Fast PDE Solver
Going Infinite: Integral Operators and Functional Analysis
- Norms and Operators
- Compactness
- Integral Operators
- Riesz and Fredholm
- A Tiny Bit of Spectral Theory
Singular Integrals and Potential Theory
- Singular Integrals
- Green's Formula and Its Consequences
- Jump Relations
Boundary Value Problems
- Laplace
- Helmholtz
- Calderón identities
Back from Infinity: Discretization
- Fundamentals: Meshes, Functions, and Approximation
- Integral Equation Discretizations
- Integral Equation Discretizations: Nyström
- Integral Equation Discretizations: Projection
- Demo: 2D Interpolation Nodes
- Demo: Choice of Nodes for Polynomial Interpolation
- Demo: Vandermonde conditioning
- Demo: Visualizing the 2D PKDO Basis
- Demo: Working with Unstructured Meshes
Computing Integrals: Approaches to Quadrature
- A Bag of Quadrature Tricks
- Quadrature by expansion (`QBX')
- QBX Acceleration
- Reducing Complexity through better Expansions
- Results: Layer Potentials
- Results: Poisson
- Demo: Kussmaul-Martensen quadrature
Going General: More PDEs

CAUTION!

These scribbled PDFs are an unedited reflection of what we wrote during class. They need to be viewed in the context of the class discussion that led to them. See the lecture videos for that.

If you would like actual, self-contained class notes, look in the outline above.

These scribbles are provided here to provide a record of our class discussion, to be used in perhaps the following ways:

as a way to cross-check your own notes
to look up a formula that you know was shown in a certain class
to remind yourself of what exactly was covered on a given day

By continuing to read them, you acknowledge that these files are provided as supplementary material on an as-is basis.

Computing

We will be using Python with the libraries numpy, scipy and matplotlib for in-class work and assignments. No other languages are permitted. Python has a very gentle learning curve, so you should feel at home even if you've never done any work in Python.

Running Code on your Own Computer

While running code in this online system should technically suffice to do your work for this class, you may find it useful to also install Python on your own computer.

The recommended way of doing so involves downloading the Anaconda Python distribution. Note that this is a commercial product (even if it is free of charge), and this is not intended as an endorsement of the company or the product. Note that we cannot promise to provide technical support for this installation.

Download Anaconda Python »

Another way to run Python code is through an online JupyterLab available through the course. Go to https://relate.cs.illinois.edu/lab get started. NOTE that this environment runs entirely in your browser. If you clear your browser data, any work 'saved' there will be irretrievably lost.